Central Winger: "Luck" vs. skill as it pertains to goals

"Luck" is a ubiquitous, catch-all term that seems to slip out of our mouths when describing a goalscoring scenario. Sometimes we characterize a a goal as resulting from a lucky shot or an advantageous deflection. Likewise, we are often caught talking about "unlucky" bounces and characterizing crossbar deflections as "deserving of a goal."

I don't think we're always wrong, but I do think we're very misguided. In my experience, there tends to be a rampant bias in attributing luck. For accredited goalscorers, "lucky" goals have the tendency to be characterized as having resulted from tremendous skill. For non-prolific goalscorers, we tend to characterize their goals as a result of mere circumstance. This is an example of confirmation bias at its finest.
Luck is random. Bountiful goalscorers gain and lose from luck at exactly the same rate as any other player.
In defense, it's often claimed that good players "create their own luck." This is not true. In this old adage, the gains that are being attributed to luck are actually the effects of unmodeled circumstance. Let me demonstrate.
Central Winger: Can "luck" and skill be separated in soccer?

The following illustration is paraphrased (and simplified) from an email exchange between myself and leading soccer analytics expert Simon Gleave – author of Scoreboard Journalism.

Let's create a rough model for shooting:
Quality of a shot multiplied by weighting coefficient = the chance a goal being scored
And, since our results are either 1 or 0 (Goal or No Goal), "Luck" is the difference between the result and the chance of a goal being scored.
Luck = result – percentage chance of goal
However, in this example, we don't control for the strength of the goalkeeper. The variance that the goalkeeper brings to the function is currently being attributed as a part of "luck."
So, we construct our model again to compensate for the goalkeeper:
Quality of the shot multiplied by weighting coefficient A + Quality of the goalkeeper multiplied by weighting coefficient B =  the chance a goal being scored
Now that we are more accurately modeling the situation, the role that skill plays in the outcome's variance is more. "Luck," reflexively, becomes less important.
We can continue this process by adding obvious variables such as game context all the way down to the coefficient of friction between the goalkeeper's particular brand of glove and the ball's surface material. As the number of variables that we don't account for approaches zero – the amount that luck plays in a given situation also approaches zero.
Since accounting for every single variable is impossible, could luck simply be the variance brought to our system by the variables that our model doesn't account for? Or even variables that are incomprehensible? I think so.
By constructing the most elementary model described above using shot information such as distance, location, shooting angle and other variables such as if the shot was the result of a header, we can estimate the likelihood of each particular shot resulting in a goal.

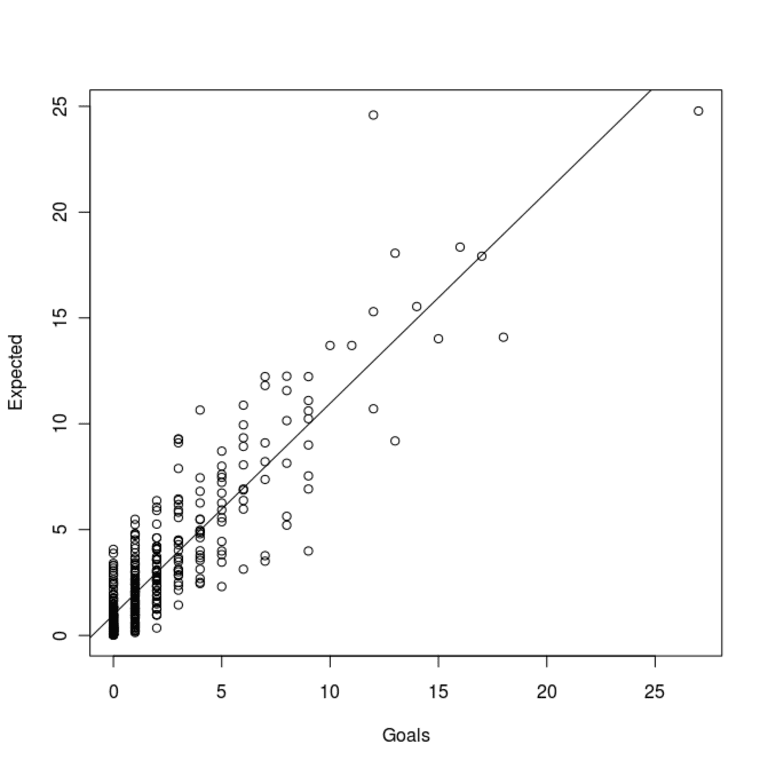
Even this elementary model is pretty good. In fact, it accounts for 79 percent of all goal-scoring variance on a player-by-player basis across MLS in 2012. The resulting line of best fit has a slope of 0.97 – which suggests that the model is slightly biased toward higher expected goal counts.

Using this model, we can attribute the differences between predicted and actual results as a combination of both luck and unmodeled variance (which includes unmodeled skill). Also, understand that each player's actions are a byproduct of the system that they operate in. Team context firmly belongs in the unmodeled skill factor as well.
Here are the top scorers in MLS last season along with their expected goal counts:

In 2012, Chris Wondolowski not only scored the most goals in MLS, he also had the highest expected goal number according to this model. I wouldn't call his strong season "lucky" by any stretch of the imagination.

Kei Kamara (above), on the other hand, had more of a difference between his expected goal rate and his actual goal rate than any other player. Kei's difference is actually twice as much as any player in MLS.
Results like this illustrate the grain of salt that one is required to take with this type of analysis. While not all of Kamara's difficulties this season can be attributed to skill, not all of his difficulties can be attributed to poor luck, either.